Cartografiando el Cosmos (II)* La estructura fractal del Universo.
Angel Requena y Abilio Orts. anrevil@terra.es y aorts2@pie.xtec.es
 | Desde que el hombre tiene conciencia de su existencia en el Universo ha sentido la necesidad de situarse dentro de él. En la actualidad los avances tecnológicos han mejorado ostensiblemente el conocimiento de la esfera celeste. Pero esa curiosidad que llevó al hombre a indagar en el cosmos sigue siendo todavía hoy una necesidad vital para muchos así como la principal fuente de nuevos descubrimientos. La aparición de la geometría fractal está permitiendo el estudio de configuraciones espaciales difícilmente abordables con los elementos de la geometría clásica. |
Introducción
Cuando en una noche estrellada miramos en cualquier dirección vemos miles
y miles de estrellas que parecen estar dispuestas entre sí de una forma
aleatoria, o al menos, eso nos parece a nosotros. Pero nada tan lejos de la realidad,
si nos fijamos un poco empezamos a discernir pequeñas agrupaciones de estrellas
u otros cuerpos por doquier como si de diferentes estructuras se trataran.
Claro que desde aquí la Tierra poco podemos decir del resto de cuerpos; conocemos muy bien la estructura y evolución de nuestro planeta, y nos atreveríamos a afirmar que tenemos un conocimiento importante de nuestros vecinos los planetas del sistema solar. Pero, ¿y del resto del universo? ¿Cómo se estructura? ¿Y por qué se estructura así?.
En este artículo intentaremos explicar el cómo y para ello usaremos una simplificación de la realidad a través de un modelo. El porqué será una tarea más difícil que, al menos en este artículo, dejaremos sin abordar; dejaremos a los científicos profesionales la responsabilidad de mojarse en una cuestión en la que actualmente sólo podemos teorizar.
En estos últimos años los investigadores han progresado enormemente en el estudio de la estructura del universo. El Universo de hoy en día poco tiene que ver con el de principios de siglo, atrás han quedado los tiempos en que no se sabía si nuestra propia galaxia era el confín del universo.
Estructura a gran escala
Y, ¿qué
sabemos realmente de la organización de nuestro Universo?. En 1986, un
grupo de astrónomos del Centro de Astrofísica Harvard-Smithsonian
(CfA), publicaron un sorprendente trabajo en la prestigiosa revista Astrophysical
Journal. Midiendo los corrimientos al rojo de cientos de galaxias en el interior
de una "rodaja" de cielo en la zona de Coma, fueron capaces de determinar
la ubicación tridimensional de la materia visible hasta una profundidad
de 500 millones de años-luz. O lo que es lo mismo, trazaron el primer mapa
tridimensional del cielo y el resultado no les dejó indiferentes. De acuerdo
a este mapa en 3D, los objetos no estaban distribuidos de una forma aleatoria
sino que más bien se ajustaban a un diseño que a todos les resultaba
familiar: su estructura era similar al de una esponja.
Los científicos encontraron filamentos, láminas, paredes y agujeros vacíos de materia que observados en su aspecto global adquirían esa estructura esponjosa. Para que lo entendamos mejor, la rodaja del CfA se parecía mucho a un trozo de queso de "gruyére". Los agujeros estaban vacios de materia (de queso en este caso) con lo que todo el queso se acumulaba en forma de finas láminas. En alguna de esas miles de millones de láminas se encontraba nuestra galaxia con nosotros dentro, claro (ver figura 1).
 | Fig.1: “Rodajas de Universo” desde el observatorio de Las Campanas (Chile). |
A este estudio le siguieron otros aún más ambiciosos y todos evidenciaron lo mismo; miraras hacia donde miraras toda la materia se estructuraba en forma de esponja, jabonaduras o si queremos también llamarlas pompas de jabón. Un descubrimiento que sorprendió enormemente a los científicos fue el de la Gran Muralla. Como ocurre con su homónima china, esta colosal lámina de galaxias se extendía a lo largo de cientos de millones de años luz. A éste le siguió otro descubrimiento que sorprendió todavía más a los científicos: el Agujero de Boötes. Se trata de una estructura casi esférica en cuyo interior apenas si encontrábamos galaxias. ¿Se imaginan un agujero en el que cabrían mil millones de galaxias como la nuestra y prácticamente vacío?. Pero lo paradójico es que este agujero no era más que uno entre cientos de millones en todo el Universo.
Recapitulando un poco tenemos un Universo lleno de agujeros en cuya "superficie" encontramos toda la materia conocida (galaxias, cúmulos, etc.). Además de eso, los filamentos, paredes y láminas de materia están regularmente esparcidas por todo el Universo. Se podría resumir diciendo, que la estructura del Universo es ubicua1.
Pero no sólo este hecho revolucionó las teorías cosmológicas hasta ese momento. Se descubrió además que estas "pompas de materia" tenían movimiento propio además de la expansión "normal" de Hubble.
Fue a finales de los años 80 cuando un grupo de científicos apodados los 7 samurais descubrieron un movimiento peculiar2 a gran escala. Estudiando la luz que emitían un grupo de galaxias elípticas consiguieron demostrar que todo el cúmulo de Virgo (incluída nuestra galaxia) está moviéndose en dirección de otro gran cúmulo, el de Hidra-Centauro. Y no sólo se mueve nuestro cúmulo en esa dirección sino que el supecúmulo de Hidra-Centauro también se mueve a gran velocidad pero en sentido contrario. Se trata pues de una "atracción mutua" entre dos supercúmulos galácticos. Pero ésto no acaba aquí ya que a su vez estos cúmulos se mueven conjuntamente a una ¡velocidad de 600 km/s! (M. Riordan, D. Schramm, Las Sombras de la Creación (Madrid, 1994)).
Se cree que, al igual que ocurría con la atracción de los cúmulos, una gran masa de materia es la responsable de esta velocidad peculiar. Se trataría de una gran agregación de materia situada más allá del supercúmulo de Hidra-Centauro y a una distancia de 150 millones de años luz y de nombre "Gran Atractor". Contiene una cantidad de materia equivalente al peso de mil billones de veces la masa del Sol, de ahí que nos está precipitando a una velocidad de vértigo en dirección al cúmulo de Hidra-Centauro (ver figura 2).
Por tanto el rompecabezas cósmico se complicaba un poco más. Nuestro universo no sólo se comporta como un gran pastel de pasas (A. Requena, "La Huella del Universo" HUYGENS 29 (2001)) al hornearse. Ahora al movimiento de la masa cocida hay que unirle el movimiento propio de las pasas (galaxias, cúmulos, etc.), independiente del movimiento producido por el horneado (expansión del Universo).
Se podría pues resumir diciendo que la estructura esponjosa a gran escala del Universo no es estática como la gomaespuma, ni se expande uniformemente como un pastel de pasas cociéndose en el horno sino que se agita adelante y atrás como si de la espuma de mar se tratara (M. Riordan, D. Schramm, Las Sombras de la Creación (Madrid, 1994)).
Hay sin embargo, otro enfoque que darle a la cuestión además del puramente físico. Si describimos la estructura a gran escala en términos geométricos nos encontramos con una estructura aparentemente esponjosa. Pero si le ponemos números a todo ésto y le damos un enfoque puramente estadístico nos llevaremos una grata sorpresa.
Función
de correlación
James Peebles, junto con otros científicos,
dejaron de lado los modelos geométricos en los que todo el mundo se centraba
en ese momento y apuntaron hacia una descripción basada en términos
matemáticos. Analizaron y cuantificaron la separación entre las
galaxias y se dieron cuenta que éstas no estaban distribuidas al azar;
existía una cierta probabilidad de encontrar cerca un par de ellas. Además
esta probabilidad, conocida también como función de correlación
de dos galaxias, era inversamente proporcional a la potencia 1´8, o lo que
es lo mismo, era proporcional a 1/r1´8.
Parece razonable pensar que esta función de probabilidad puede tener algo que ver con la archiconocida fuerza de gravedad que como bien sabemos es inversamente proporcional al cuadrado de la distancia, o también viene dada por la expresión matemática 1/r2.
| Fig.2: Movimientos peculiares en nuestro rincón del universo. todo el grupo local se mueve junto con los supercúmulos de Virgo e Hidra-Centauro hacia el Gran Atractor, tomado de “Las sombras de la Creación”, acento ed., página 123. |
Y en cierto modo esta coincidencia no era del todo casual aunque como ahora veremos no era la única explicación a esta enigmática correlación. Durante los años 80 un grupo de científicos americanos y soviéticos comenzaron a aplicar los modelos estadísticos de Peebles a los cúmulos galácticos y tropezaron con un hecho muy curioso. Los cúmulos parecían estar más estrechamente correlacionados que las galaxias y vieron que esa correlación era también proporcional a 1/r1´8 (M. Riordan, D. Schramm, Las Sombras de la Creación (Madrid, 1994)).
¡Qué coincidencia!. El mismo valor que en el caso de las galaxias. Y no sólo eso, descubrieron algo ciertamente desconcertante. La probabilidad de que encontráramos juntos dos cúmulos ricos era superior a la de encontrar dos cúmulos ordinarios o incluso dos galaxias cualesquiera. Si consideramos el hecho de que los cúmulos ricos no son objetos muy comunes en el universo podemos intuir que la correlación de estos cúmulos no sólo responde a cuestiones gravitatorias.
Parece lógico pensar que en un universo gobernado únicamente por la gravedad la distribución más probable sería la distribución aleatoria en la que las galaxias estarían igualmente dispuestas en arracimamientos que aisladamente (ver figura 3). Sin embargo viendo los mapas obtenidos de las diferentes mediciones se observa claramente que las galaxias y con ellas los cúmulos no se distribuyen al azar sino que más bien tienen tendencia a agruparse (ver figura 4).
| |
 |
| Fig.3: Distribución aleatoria
de galaxias. | Fig.4: Agrupación
de galaxias. |
Por tanto podemos aseverar que la gravedad por sí sola no es capaz de explicar este misterio. Debe haber algo más aparte de ésta que determine la estructura a gran escala del universo, quizá el modelo fractal nos ayude a entenderlo.
Naturaleza fractal
La geometría trata del estudio de las formas. Para ello recurre a modelos
sencillos, o por lo menos, no tan complejos como la realidad. La geometría
clásica (la que recopiló Euclides en sus Elementos) reduce cualquier
figura a rectas, planos, circunferencias, etc. Sin embargo esta geometría
comenzó a ser cuestionada por la rotundidad de uno de sus cinco postulados,
el de las paralelas (por un punto exterior a una recta dada pasa una única
paralela). Así de esta forma, sustituyendo este postulado por la posibilidad
de infinitas rectas o bien la imposibilidad de paralelas, aparecieron las diferentes
geometrías no euclídeas (que entre otras cosas permitieron a Einstein
desarrollar su teoría de la relatividad).
Como hemos dicho, la geometría proporciona modelos que permiten estudiar la realidad. La validez de dichos modelos depende de su “ajustabilidad” al original, es decir, de su capacidad de explicación de la realidad. Un ejemplo muy claro puede verse en el tránsito del geocentrismo al heliocentrismo: el modelo geocentrista no podía explicar fenómenos observables como el diferente brillo y tamaño de una estrella según la estación del año o el paralaje (A. Koestler Los sonámbulos, Salvat Ed. (Barcelona, 1989)).
Un caso similar motivó la necesidad de la geometría fractal, aunque si bien en este caso no se trata de la sustitución de un modelo por otro sino de la convivencia de ambos modelos (dependiendo de la naturaleza del problema utilizaremos un tipo de modelo u otro). A finales del siglo XIX, aparecieron diferentes “monstruos matemáticos” que desafiaban la lógica euclídea. Se hacía necesaria la búsqueda de modelos metodológicos fuera de la geometría euclídea que permitieran el estudio de estos entes matemáticos. En este artículo nos vamos a detener en su estudio y en la solución que aportó el matemático francés Benoït Mandelbrot. Éste comprobó que tras la irregularidad de todos estos objetos se escondía un concepto clave: la autosemejanza interna. Así, en 1967, esboza por primera vez en uno de sus artículos lo que hoy conocemos como geometría fractal y que, posteriormente en 1975, daría a conocer en su obra Los objetos fractales. Forma, azar y dimensión (B. Mandelbrot, Los objetos fractales. Forma, azar y dimensión, Ed. Tusquets (Barcelona, 1975)).
La geometría fractal es revolucionaria, innovadora e incluso, en sus orígenes, escandalosa. La principal novedad reside en la introducción de un concepto de dimensión geométrica que no tiene por qué ser un número natural. Así, la geometría euclidiana asigna al punto dimensión cero, a la recta dimensión uno, dos a las superficies planas y, por último, dimensión tres a las curvas alabeadas.
Este nuevo tratamiento de la dimensión permite no sólo hablar de dimensiones fraccionarias. También es posible asignar un número irracional a la dimensión fractal de un conjunto.
Pero, ¿qué es un fractal?
Mandelbrot estudió
todos estos objetos irregulares de los que hablábamos anteriormente y los
designó mediante un neologismo latino: fractal, del latín “fractus”
que significa interrumpido o irregular y sigue siendo así a cualquier escala.
El gran acierto de Mandelbrot fue comprobar que la naturaleza está llena de estructuras fractales: “... objetos naturales muy diversos, muchos de los cuales nos son familiares, tales como la Tierra, el Cielo y el Océano, se estudian con la ayuda de una amplia familia de objetos geométricos que hasta ahora habían sido considerados esotéricos e inutilizables, pero que espero poder demostrar, por el contrario que, por la simplicidad, la diversidad y la extensión extraordinaria de sus nuevas aplicaciones merecen ser integrados pronto en la geometría elemental” (B. Mandelbrot, Los objetos fractales. Forma, azar y dimensión, Ed. Tusquets (Barcelona, 1975)).
| Foto 5: Si consideramos cada ramificación por separado observamos que es similar a todo el relámpago. Tormenta de rayos en Tucson, Arizona, tomada de “Fotografiando la naturaleza” Ed. Carroggio, página 81. |
El paso del tiempo ha demostrado que Mandelbrot estaba en lo cierto: las líneas de las costas, las redes fluviales, las galaxias, el perfil de las montañas, los conductos pulmonares, los cráteres de la luna o los vasos sanguíneos son algunos de los innumerables ejemplos de estructuras a priori complicadas pero que la geometría fractal ha desvelado que no lo son tanto.
Pero, ¿qué es lo que caracteriza a estas estructuras? Al analizarlas podemos comprobar que todas ellas presentan una irregularidad que hizo que nadie se “atreviera” a estudiarlas durante años. Sin embargo, Mandelbrot encontró que los grados de irregularidad que corresponden a distinta escala son, de alguna forma, iguales. Es decir, parece como si el mismo mecanismo, el mismo patrón hubiera podido engendrar tanto los pequeños detalles como los grandes. Esta propiedad esencial en la teoría fractal se denomina autosemejanza u homotecia interna, es decir, cada “pedazo” es, estadísticamente hablando, homotético (de igual forma) al “todo”.
Perrin en el prólogo de su obra “Les Atomes” (1913) evoca unos objetos familiares de forma irregular o interrumpida y así expresa que la geometría de la naturaleza es caótica y está mal representada por el orden perfecto de las formas usuales de Euclides o del cálculo diferencial.
Recogiendo estas palabras Mandelbrot caracteriza la geometría fractal por dos elecciones: la elección de problemas en el seno de la naturaleza y la elección de herramientas en el seno de las matemáticas.
De esta forma “entre el dominio del caos incontrolado y el orden excesivo de Euclides, hay a partir de ahora una nueva zona de orden fractal” (Mandelbrot, op. cit. página 18).
Conjuntos de estructura fractal
Existen
muchos procesos en la naturaleza que conducen a formas irregulares. Son, por ejemplo,
los procesos de separación de fronteras entre dos medios en los que se
observan incursiones de un medio en otro. Si aumentamos la escala de dicha frontera
las incursiones aumentan indefinidamente. Podemos encontrar ejemplos de este tipo
de fenómenos en la región donde entran en contacto dos medios como
puede ser el agua de un río y la tierra o las líneas de costa. Otro
tipo de procesos que conducen a formas irregulares son los procesos de ramificación
en los que un objeto se va reemplazando por otro número de objetos similares
a él en forma y que dan lugar a estructuras de tipo arbóreo, raíces,
estructuras coralinas, etc. Por último cabe citar, también, los
procesos de formación de la porosidad que dan lugar a objetos que contienen
poros o “islas” de otro objeto en su interior, tal es el caso de las
nubes.
| |
|
|
| Fig. 6: Diferentes ejemplos de procesos de separación de fronteras, de ramificación y de porosidad, tomada de “Estructuras fractales”, pág. 3. | ||
La geometría diferenciable propone modelos adecuados a una cierta regularidad y permite aproximar las formas geométricas más complejas mediante otras más simples: rectas, planos, etc.
Pero, por ejemplo, un observador terrestre podría admitir que la esfera es un modelo adecuado para la luna. Sin embargo, para un astronauta que se encuentra sobre ella y puede observar los diferentes cráteres, este no sería un modelo válido.
Así, la geometría fractal ofrece un modelo alternativo al de la geometría clásica basado en las relaciones entre el objeto y sus partes a diferentes escalas, sin necesidad de recurrir a otras formas geométricas (esferas, planos, cilindros) exteriores a él. La geometría fractal busca y estudia los aspectos geométricos que son invariantes con el cambio de escala (esta invarianza nos permitirá definir el concepto de dimensión fractal).
Aunque es difícil dar una definición general de fractal porque muchas de ellas no se pueden aplicar a todas las familias de fractales existentes, tal vez la mejor forma de describirlos consista en señalar lo que tienen en común los procesos matemáticos que los generan. Al fin y al cabo, lo más interesante de los fractales y la raíz de sus propiedades matemáticas más profundas se encuentra en la forma típica de la estructura de los procesos que les dan origen.
Así, un fractal viene a ser el producto final que se origina a partir de la iteración infinita de un proceso geométrico bien definido. Este proceso geométrico elemental, generalmente de naturaleza muy simple, determina la estructura final que debido a la repetición infinita da lugar a estructuras de una complicación aparentemente extraordinaria.
De esta forma la geometría fractal constituiría un paso intermedio entre la geometría clásica y el análisis moderno, utilizando como éste los procesos infinitos. Así, a las consideraciones de naturaleza estática de la geometría clásica incorpora el dinamismo de los procesos infinitos del paso al límite. (Guzmán, M. y otros, Estructuras fractales y sus aplicaciones, Ed. Labor (Barcelona 1993)).
A continuación describimos algunos de los conjuntos fractales más importantes: el conjunto de Cantor, la curva de Koch y el conjunto de Besicovitch.
Para construir el conjunto de Cantor partimos del segmento (0,1), lo dividimos en tres partes iguales y eliminamos el segmento central. Con cada uno de los dos segmentos restantes realizamos la misma operación y así infinitamente. El conjunto de puntos que quedan después de las iteraciones es el conjunto de Cantor.
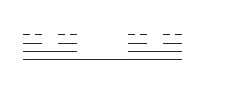 | Fig. 7: En el gráfico se pueden observar las cuatro primeras iteraciones del conjunto de Cantor realizadas con el asistente matemático “DERIVE”. |
Vamos a analizar el conjunto de Cantor: en la primera fase eliminamos la tercera parte del intervalo unidad (0,1). En la segunda fase eliminamos dos segmentos de longitud un noveno, y así en la fase n-ésima eliminamos 2n-1 segmentos de longitud 1/3n. Si realizamos la resta de la longitud inicial 1 menos los diferentes segmentos que vamos eliminando en cada fase de construcción del conjunto obtenemos que el conjunto de Cantor tiene longitud 0.
Por otra parte, podemos renombrar los números del intervalo (0,1) en base 3 del modo siguiente: si el número está en el primer tercio del segmento, le asignamos el valor 0, si está en el tercio central le asignamos el valor 1 y un 2 si está en la última parte. De esta forma todo número del citado intervalo está representado por una secuencia 0’abc... donde a, b, c son valores del conjunto {0,1,2}. Los números del conjunto de Cantor serán aquellos que no tengan ningún 1 en su representación (el valor 1 corresponde al tercio central que se elimina en cada iteración). Así hemos demostrado que existe un número infinito no numerable de puntos (todos los que están formados por los valores 0 y 2).
Es decir, hemos construido un conjunto de longitud nula que contiene un número infinito de puntos. En otras palabras, un conjunto pequeño pues tiene longitud cero pero grande pues contiene infinitos puntos.
La curva de Koch nos permitirá estudiar procesos de separación de fronteras. Para su construcción partiremos del segmento (0,1). En la primera fase dividimos dicho segmento en tres partes iguales, eliminamos la parte central sobre la que hemos construido un triángulo equilátero. A continuación repetimos el proceso indefinidamente sobre cada segmento.
| Fig. 8: Cuatro primeras iteraciones de un copo de nieve de Koch tomadas de “El turista matemático”, I. Peterson, Alianza Ed., Madrid, 1992, pág. 139. Si observamos la línea de costa a escala 1/100 encontramos una serie de bahías y penínsulas, examinándola a escala 1/1.000 observamos un conjunto de subbahías y subpenínsulas. |
Podemos partir inicialmente, en lugar del segmento inicial (0,1), de un triángulo equilátero y realizar las iteraciones sobre cada uno de los lados, obteniendo la curva de Koch o cristal de nieve.
La curva de Koch tiene la propiedad de que a pesar de encerrar un área finita, pues puede encerrarse dentro de un cuadrado del que podemos conocer su área, tiene una longitud infinita, pues en cada iteración de construcción la curva aumenta según una relación de 4/3 y por tanto para sumar los lados debemos sumar los términos de una progresión geométrica de razón 4/3 cuya suma es infinita. He aquí su carácter de monstruo geométrico.
Otro fractal de reconocida importancia es el conjunto de Besicovitch para cuya construcción partimos de un cuadrado de lado unidad. A continuación, lo dividimos en cuatro partes iguales eliminando los cuadrados inferior derecha y superior izquierda. Los otros dos cuadrados se dividen en cuatro cuadrados iguales eliminando ahora los cuadrados superior derecha e inferior izquierda. Así quedan cuatro cuadrados de lado 1/4 en la primera como resultado de esta primera fase. A partir de aquí se repite el proceso en cada uno de estos cuadrados.
| Fig. 9: En el gráfico se pueden observar las tres primeras iteraciones del conjunto de Besicovitch tomadas de “Aventuras matemáticas”, Guzmán, M:, Pirámide, Madrid, 1995, pág. 225. |
El conjunto de Besicovitch nos proporciona un modelo para estudiar procesos de estructura porosa.
| Fig. 10: Triángulo de Sierpinski tomado de “El turista matemático”, pág. 142. | |
| Fig. 11: Tamiz o alfombra de Sierpinski tomado de “El turista matemático”, pág. 143. |
Otros fractales famosos que permiten estudiar fenómenos de porosidad son el triángulo de Sierpinski (a partir de un triángulo equilátero eliminamos, en cada iteración, el triángulo central obtenido al unir los puntos medios de cada lado), el tamiz o alfombra de Sierpinski (tomando cuadrados en lugar de triángulos) o la esponja de Menger (fractal tridimensional sustituyendo los cuadrados por cubos).
| Fig. 12: Esponja de Menger tomado de “El turista matemático”, pág. 144. |
Dimensión fractal
El concepto de dimensión
es clave en todo el entramado de la geometría fractal. Como hemos expuesto
anteriormente rompe con todos los esquemas establecidos hasta el momento. Todo
conjunto geométrico y, por tanto, todo objeto natural tiene un grado de
irregularidad o fragmentación. La dimensión fractal es el número
real que cuantifica dicha irregularidad. Frente al concepto simplificado de dimensión
euclidiana, la dimensión fractal está dotada de continuidad aceptando
cualquier valor entre 0 y 3.
Los objetos naturales están formados por muchas partes. El concepto de homotecia interna (semejanza de dichas partes respecto del total) de los objetos fractales nos permitirá definir la dimensión fractal.
Para definir la dimensión fractal o de homotecia utilizaremos ejemplos sencillos. Para ello, vamos, en primer lugar, a establecer la relación entre el número N de partes iguales en que dividimos una figura, la razón de homotecia r que convierte el todo en cada una de esas partes y la dimensión D de dicha figura.
Ejemplo 1: Consideramos un segmento dividido en 3 partes iguales:
![]()
N=3
(hemos dividido el segmento en tres partes iguales), r =1/3 (la longitud de cada
trozo es la tercera parte de la longitud total), D=1 (pues se trata de un segmento).
Así, se cumple: N = (1/r) elevado a D
Ejemplo 2: Consideramos un cuadrado dividido en 9 partes iguales:
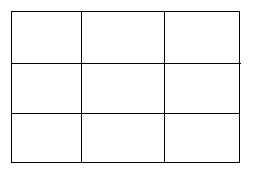
N=9 (hemos dividido el cuadrado en nueve partes iguales), r =1/3 (el área
de cada cuadradito es la tercera parte del área total), D=2 (pues se trata
de un cuadrado).
Así, se cumple: N = (1/r) elevado a
D
Ejemplo 3: Consideramos un cubo dividido en 8 partes iguales:
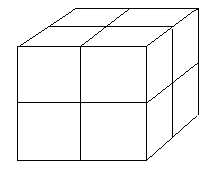
N=8 (hemos dividido el cubo en ocho partes iguales), r =1/2 (el volumen de cada cubito es la mitad del volumen total), D=3 (pues se trata de un cubo).
Así,
se cumple: N = (1/r) elevado a D
Es decir,
en cualquier caso obtenemos la misma relación. A partir de ella podemos
despejar la dimensión D (tomando logaritmos) obteniendo la dimensión
de homotecia:
D = log N / log (1/r)
Así pues podemos
calcular la dimensión de los fractales anteriores:
El conjunto de Cantor tiene dimensión igual a 0'6309 (es decir mayor que un punto pero menor que una recta) pues N=2 (tomamos dos subintervalos) y r=1/3 (cada subintervalo es la tercera parte del anterior).
El cristal de nieve de Koch tiene dimensión 1'2619 (entre una recta y un plano) pues N=4 (en cada iteración se forman cuatro segmentos) y r=1/3 (cada segmento es la tercera parte del lado del triángulo de la iteración anterior).
El conjunto de Besicovitch tiene dimensión 1 (se trata de un conjunto plano que contiene rectas en todas las direcciones y sin embargo tiene área nula) pues N=16 (cuadraditos) y r=1/16 (el área de cada cuadradito es la dieciseava parte del cuadrado de la iteración anterior).
Fractales aleatorios
Hasta este momento únicamente
se han tenido en cuenta fractales de tipo determinista, es decir, aquellos en
los que el azar no aparece en el proceso de formación. Sin embargo, estos
fractales tan “rígidos” no se adaptan, y por tanto no sirven
como modelo de la gran mayoría de procesos naturales.
Por esta razón y, partiendo de un determinado fractal, podemos establecer diferentes variaciones debidas al azar. Son los llamados fractales aleatorios. Por ejemplo, en la construcción del conjunto de Cantor eliminamos el segmento central de longitud m, donde m puede ser una variable aleatoria uniforme que tome valores entre 0 y 1 o bien, en la curva de Koch, podemos sustituir los triángulos equiláteros por isósceles o, incluso, permitir que en lugar de levantar el triángulo hacia fuera pueda construirse hacia dentro. De esta forma, por ejemplo, podemos construir modelos para diferentes sistemas montañosos.
| Fig. 13: Modelos montañosos a partir de fractales aleatorios tomada de “Estructuras fractales”, pág.65. |
Otro ejemplo de fractal
aleatorio se obtiene sustituyendo los cuadrados del conjunto de Besicovitch por
círculos de radio aleatorio (tamiz apoloniano).
| Fig. 14: Tamiz apoloniano tomado de “Los objetos fractales”, pág. 79. Mandelbrot lo utiliza como modelo para estudiar los cráteres de la luna. Los centros de los círculos se toman de forma aleatoria (según una distribución probabilística del modelo Poisson) y los radios se eligen de forma que se asegure la homotecia interna., pág.65. |
Pero si lo que se busca es una irregularidad máxima frente
a esta suave irregularidad de los modelos fractales anteriores podemos recurrir
al movimiento browniano.
El botánico británico Robert Brown descubrió en 1827 que las partículas de polen en disolución acuosa describían un movimiento que era una sucesión de pequeños desplazamientos mutuamente independientes e isótropos (todas las direcciones son igualmente probables).
Albert Einstein publicó en 1905, el mismo año en que publicó su teoría de la relatividad, un estudio matemático del movimiento browniano basado en la teoría cinética de los gases y que permitió a Perrin calcular el número de Avogadro (Guzmán, M. y otros, Estructuras fractales y sus aplicaciones, Ed. Labor (Barcelona 1993)).
El movimiento browniano describe una curva que, a semejanza de la de Koch, es continua en todos los puntos y al mismo tiempo no es diferenciable en ningún punto. La autosemejanza interna no es, en este caso, de tipo geométrico sino estadístico. Una particularidad muy interesante del movimiento browniano es que se trata de una curva que rellena una superficie (igual que la curva fractal de Hilbert) y por tanto su dimensión fractal es 2.
| Fig. 15: El movimiento browniano es una sucesión de pequeños desplazamientos en cualquier dirección sin ninguna norma, es decir, se trata de un movimiento caótico que puede estudiarse como un fractal estadístico. Ilustración tomada de “Estructuras fractales” pág 60. |
Mandelbrot introdujo los llamados movimientos brownianos fraccionarios que permiten variaciones más o menos suaves del movimiento original y permiten modelizar diferentes situaciones como montañas, líneas de costas (eliminando la excesiva irregularidad) o crecidas y estiajes de diferentes ríos, donde variando un determinado parámetro H podemos modelizar ríos como el Nilo donde el crecimiento es más suave (H=0'9) u otros como el Rin o el Loira (H=0'5) (B. Mandelbrot, Los objetos fractales. Forma, azar y dimensión, Ed. Tusquets (Barcelona 1975)).
Compresión de imágenes
Uno de los aspectos más importantes de la geometría fractal es la
posibilidad de tomar una imagen y expresarla mediante un sistema de funciones
iteradas, ésto es, expresar una imagen como un conjunto de funciones que
se comportan como un fractal. El mayor problema es encontrar el sistema de funciones
que describa la imagen3. La introducción del ordenador ha permitido sustituir
el lápiz del geómetra clásico por el ordenador. Así,
como resultado de esta interacción el profesor M.F. Barnsley probó
el teorema del collage, en 1986, que permite aproximar, mediante fractales, una
imagen descomponiéndola en partes de forma que cada una de ellas se puede
obtener a partir de la imagen total mediante una aplicación contractiva
(mantiene la forma y cambia el tamaño).
| Fig. 16: Una imagen real puede ser generada mediante fractales a partir de una sucesión de funciones iteradas, tomada de “El turista matemático” pág 153. |
Y además podemos simular el movimiento de dichas imágenes mediante una serie de transformaciones afines (giros, traslaciones, simetrías, homotecias).
| Fig. 17: El ordenador permite simular el movimiento de las imágenes a partir de transformaciones del sistema de funciones iteradas que definen el fractal que genera la imagen. Imagen tomada de Estructuras fractales, pág. 200 y 206. |
Universo Fractal
El principio cosmológico
formulado por Einstein afirma que el universo es homogéneo e isótropo.
Es decir, el universo se comporta de forma uniforme, posee las mismas propiedades
en cualquier punto del espacio y en cualquier instante y, por tanto, no hay ninguna
región privilegiada (al contrario de lo que se pensó durante gran
parte de nuestra historia, dotando a la Tierra de unas cualidades que en absoluto
le pertenecían). Sin embargo, se trata de un principio y, por tanto, necesita
ser comprobado experimentalmente.
Las últimas observaciones cuestionan su veracidad hasta el punto de que, aunque la mayoría de los científicos aceptan su validez, está siendo fuertemente cuestionado por otros (entre ellos podemos citar a Benoit Mandelbrot, Los objetos fractales cap. 6: 'La distribución de las galaxias' o Gérard de Vaucouleurs, "The case of a hierarchical cosmology" Science 167, pp. 1203-1213 (1970).
| Fig. 18: Algunos fractales destacan por su belleza como el dragón de Mandelbrot, tomada de “www.quanta.net”. |
En los últimos años las observaciones parecen encaminar a los astrofísicos a la asunción de un modelo jerárquico de tipo fractal para explicar las agrupaciones de estrellas en galaxias, de éstas en cúmulos y así sucesivamente. Quizás el problema radique en cómo conjugar ambos modelos, es decir, dónde es válido uno y dónde debe utilizarse el otro.
 | Fig. 19: Modelo de Universo sembrado de Mandelbrot. Para corregir el excesivo tamaño de los vacíos introduce el concepto de lagunosidad de un fractal (mordisco espacial cuya forma no necesariamente debe ser esférica, como en la esponja de Menger). |
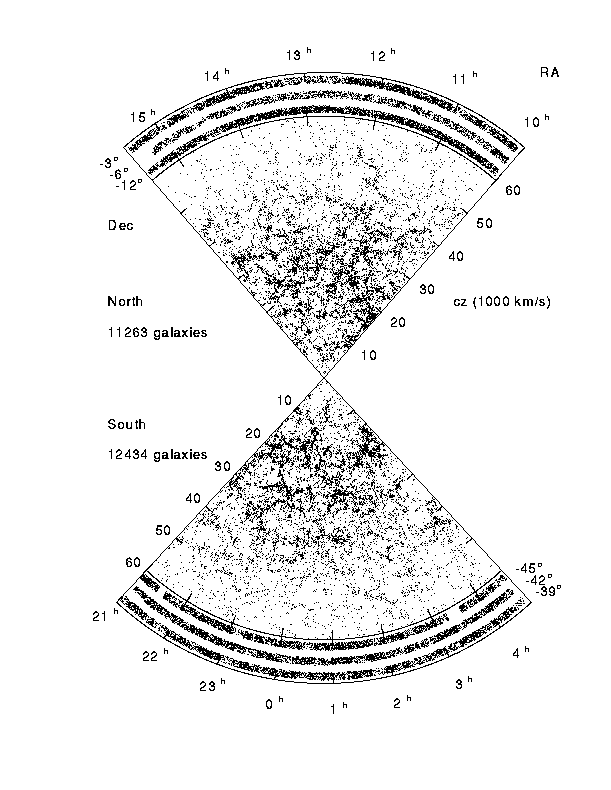
Hay algunos datos que parece que pueden esclarecer este asunto. Así, comparando diferentes porciones del espacio (en concreto la rebanada meridional del catálogo de "Las Campanas" con la primera rebanada del Center of Astrophysics en su segunda medición, CfA2) observamos los mismos elementos hasta cierta escala. Sin embargo, a partir de una determinada profundidad, ésto no sucede (en un modelo de tipo fractal el tamaño de estas estructuras debería ser mayor para rebanadas más profundas). Es ese momento el que marca, según palabras de V. Martínez, "el principio del fin", o sea, el paso de una estructura que podríamos considerar de tipo fractal a una región en la que se alcanza la homogeneidad propuesta en el principio cosmológico (V.J. Martínez, “Is the Universe fractal?”, Science nº 284 (1999) pp. 446-447). Veamos la situación actual con un poco de detenimiento.
Como ya anticipábamos en los primeros puntos del artículo, para estudiar la distribución espacial del Universo podríamos recurrir a modelos de tipo probabilístico o a modelos geométricos. Desde el punto de vista probabilístico podemos encontrarnos ante tres situaciones: que las galaxias se encuentren distribuidas aleatoriamente en el espacio, que se encuentren agrupadas formando cúmulos o arracimamientos (clusters), o bien, que se encuentren separadas por una distancia común.
Así podemos definir una función x(r), función de correlación, que mide los clusters o agrupaciones de galaxias para una determinada región esférica de radio r. Si suponemos que las galaxias se sitúan aleatoriamente en la bóveda celeste, seguirían una distribución probabilística según el modelo de Poisson y así x(r)=0. Para una determinada zona en la que encontremos agrupaciones o arracimamientos en exceso x(r)>0 y si encontramos en defecto x(r)<0.
| Fig. 20: APM Galaxy Survey. La imagen muestra la distribución de galaxias de un área perteneciente al cielo austral y centrada en el polo sur galáctico. Las galaxias tienen unas magnitudes aparentes de en torno a la 20ª magnitud y el área escaneada representa el mayor volumen cartografiado hasta el momento. Fotografía cortesía de Steve Maddox. |
¿Cómo podemos medir esta "aglomeración" de galaxias? A partir de la expresión que relaciona la masa con el radio de la esfera considerada: d = m/V (densidad = masa / volumen). Así para una determinada región esférica de radio R, el volumen vendrá dado por: (4pR3)/3. Haciendo tender el radio a infinito podemos obtener la densidad media global.
A priori la densidad media no debería plantear ningún problema de cálculo pero, al igual que ocurre con la línea de la costa, la convergencia (el valor al que tiende la densidad media al ir aumentando el radio) no proporciona un valor concreto. A medida que ha ido aumentando la profundidad del universo alcanzado por los telescopios, la densidad no ha dejado de disminuir manteniéndose aproximadamente proporcional a RD-3, donde D es un número entero positivo menor que 3. Ésto indica que a medida que uno se va alejando de la Tierra (el centro de las esferas que estamos considerando) los objetos celestes se agrupan jerárquicamente (arracimamientos). Como dijo G. De Vaucouleurs "el arracimamiento de las galaxias y, sin lugar a dudas de todas las formas de la materia, es, según todos los métodos observables, la característica dominante de la estructura del universo, sin ningún indicio de que haya una aproximación a la uniformidad: la densidad media de la materia decrece continuamente cuando se consideran volúmenes cada vez mayores... y las observaciones no dan ninguna razón para suponer que esta tendencia no continúe a distancias mucho mayores y densidades mucho más bajas". Como se desprende de este texto, De Vaucouleurs apuesta por un universo jerarquizado a cualquier escala, es decir un universo que se ajustaría a un modelo de tipo fractal (Benoit Mandelbrot, Los objetos fractales. cap. 6: 'La distribución de las galaxias').
Otro científico que apostó por un modelo estrictamente jerarquizado (y por tanto fractal) fue C.V.L. Charlier en 1922 a partir de un modelo propuesto en 1907 por Fournier d'Albe.
Sin embargo este modelo de Fournier-Charlier es excesivamente regular y por ello resulta totalmente inverosímil. A partir de estos mimbres se ha ido perfeccionando y cada vez se están obteniendo modelos más realistas.
Mandelbrot propone un modelo fractal probabilístico a partir del movimiento browniano y con una autosemejanza aleatoria basada en una distribución de probabilidad hiperbólica para el cual D es aproximadamente 1'2. Se trata de un modelo cuyas correlaciones teóricas (las calculadas mediante la función x(r)) coinciden con las empíricas calculadas por P.J.E. Peebles en 1980.
Estudios más recientes establecen que la función de correlación
x(r) es aproximadamente:
(r/r0)-1'8 donde r0 es 5h-1 Mpc4 (h es la constante
de Hubble en unidades de 100 km s-1).
Empíricamente se puede demostrar que a partir de correlaciones observadas de las galaxias y cúmulos, éstos parecen seguir una disposición fractal, con una dimensión de alrededor de 1'2, o sea, una ordenación casi lineal. Esta dimensión 1'2 es igual además a la dimensión 3 del espacio menos 1'8, que es aproximadamente el exponente de la ley de potencias 1/r1'8 (donde r es la separación entre las dos galaxias o cúmulos) que siguen las funciones de correlación (M. Riordan, D. Schramm, Las Sombras de la Creación (Madrid, 1994)).
¿Hasta dónde es válido este modelo? Esta pregunta tiene una muy difícil respuesta. Se acepta el comportamiento fractal hasta una profundidad de 100 millones de años luz. A mayores escalas y, por las medidas de corrimiento al rojo de la galaxia Perseo-Piscis, Guzzo et al. (1991) encontraron un valor D=2'2. Pietronero et al. (1998) obtuvieron que el agrupamiento a gran escala de las galaxias está bien descrito por un modelo fractal de dimensión 2 para escalas de, al menos, 150 h-1 Mpc sin tránsito a la homogeneidad. Usando la relación masa-radio (densidad=masa/Volumen(radio)) extienden el rango fractal hasta 1000 h-1 Mpc con la misma dimensión fractal.
Otros autores como Scaramella et al. (1998) han encontrado que la distribución de las galaxias proporciona evidencias para una transición a la homogeneidad a gran escala. Así, la relación masa-radio proporciona una dimensión D=3. Es decir, estamos ante posturas incompatibles.
En opinión de Vicent Martínez, “el comportamiento fractal a pequeña escala desaparece a gran escala proporcionando evidencias de la transición a la homogeneidad pues la hipótesis fractal requiere que la longitud de correlación r0 aumente linealmente con la profundidad de la muestra”. Benoist
et al. (1996) han demostrado que r0 depende en mayor grado de la luminosidad intrínseca de las galaxias de la muestra que de la profundidad.¿Dónde está el problema? Los defensores del modelo fractal total argumentan que el tratamiento de los estimadores estadísticos utilizados para la función de correlación está basados en una asunción implícita de que la distribución espacial de las galaxias es un proceso puntual homogéneo e isotrópico. Es este quizás el punto de crucial importancia en esta controversia que refleja la diferente metodología adoptada por cada parte (V.J. Martínez, “Is the Universe fractal?” Science nº 284 (1999) pp. 446-447).
Otro argumento posible es que algunos problemas en la construcción de las muestras analizadas (Las Campanas, Stromlo-APM, ESP) podrían afectar a la validez de su análisis estadístico.
E incluso que las correlaciones entre cúmulos son todavía provisionales y pueden deberse a efectos de proyección5. Es necesario pues disponer de más muestras, mucho más amplias y sin sesgos de las estructuras a gran escala, de forma que podamos seleccionar los cúmulos y determinar lo estrechamente relacionados que están entre sí (M. Riordan, D. Schramm, Las Sombras de la Creación (Madrid, 1994)).
Como dice el profesor Martínez, "la próxima generación de inspecciones de corrimiento al rojo nos proporcionarán una respuesta más concluyente a la cuestión de la estructura a gran escala del universo. Mientras tanto, las dos corrientes deberían ponerse de acuerdo sobre las medidas estadísticas que deben cuantificarse, los estimadores más apropiados, las correcciones cosmológicas que deben aplicarse a los datos y la escala a la que el análisis estadístico puede dar resultados significativos".
Esperaremos impacientes el desenlace.
Notas
* Con este artículo
finaliza el capítulo que hemos denominado el Cartografiado del Cosmos y
que se completó con "La Huella del Universo" HUYGENS 29 (2001).
Para la perfecta comprensión del actual no será necesario releer
el anterior ya que ambos aún perteneciendo a la misma familia dentro del
campo de la cosmología, abordan temas diferentes.
1Que está
presente al mismo tiempo en todas partes.
2Aunque, tal como describió
Hubble por primera vez en 1929, el universo como un todo está expandiéndose
constantemente de un modo uniforme, existen desviaciones respecto a este “flujo
de Hubble”, denominadas velocidades peculiares.
3Obtenido de la página
de internet www.quanta.net.
4 Un megaparsec (Mpc)= 3'26 · 1026 años
luz.
5 Un cúmulo alejado puede parecer próximo a un cúmulo
cercano (a nosotros) que se encuentre en su misma dirección, o puede hacer
parecer que el cúmulo cercano sea más rico en galaxias de lo que
realmente es. Cualquiera de los dos efectos podría hacer aumentar artificialmente
la función de correlación de cúmulos ricos.
Bibliografía
M. Riordan, D. Schramm, Las Sombras de la Creación (Madrid, 1994).
A. Requena, "La Huella del Universo" HUYGENS 29 (2001).
A. Koestler,
Los sonámbulos, Salvat Ed. (Barcelona, 1989).
B. Mandelbrot, Los objetos
fractales. Forma, azar y dimensión, Ed. Tusquets (Barcelona, 1975).
M. Guzmán, y otros, Estructuras fractales y sus aplicaciones, Ed. Labor
(Barcelona 1993).
I. Peterson, El turista matemático, Alianza Ed. (Madrid
1992).
M. Guzmán, Aventuras Matemáticas, Pirámide (Madrid
1995).
Gérard de Vaucouleurs, "The case of a hierarchical cosmology"
Science 167 pp. 1203-1213 (1970).
V.J. Martínez, “Is the Universe
fractal?” Science nº 284 pp. 446-447 (1999).