Estudio estadístico de
la distancia de laTierra a las estrellas
Una aplicación de la distribución
de Bernford
Por Abilio Orts
Introducción
A menudo nuestra "intuición matemática" da por ciertos resultados que no han sido demostrados o, incluso, resultados que son falsos. No es que se pretenda rechazar la intuición sino que, a veces, grandes científicos han tenido que luchar contra los prejuicios creados por estas suposiciones a priori.
El resultado que se presenta a continuación es un claro ejemplo de lo ex-puesto anteriormente. Y como tantos otros, surge por casualidad. A finales del siglo XIX, el matemático y astrónomo Simon Newcomb (Wallace, Canadá, 1835Washington, Estados Unidos 1909) utilizando las tablas de lo-garitmos en mediciones astronómicas observó un curioso hecho: las primeras páginas estaban más usadas que las últimas. Esto que en un primer momento se explicó como una casualidad fue retomado con posterioridad por el matemático J. Bernford. Bernford formuló que la probabilidad del primer dígito no nulo de una observación no es uniforme, esto es, no es igual de probable que sea 1 ó 2, ó 3, etc.
Este hecho que "choca" con la intuición fue demostrado matemáticamente por Bernford. Esta demostración puede verse en el apartado segundo, aunque para seguir los siguientes apartados únicamente es necesario observar la tabla 1 (para poder seguirla únicamente es necesario conocimientos mínimos de probabilidad).
Finalmente, es importante aclarar que la distribución de Bernford es aplicable a datos obtenidos en la naturaleza y, evidentemente, no es aplicable a datos "producidos" por el hombre: resultados al lanzar un dado, números de lotería, etc... donde la simetría del problema lleva a modelos de probabilidad uniformes que no se corresponden con la realidad de la naturaleza.
Distribución de Bernford
La
simetría a la que nos tiene acostumbrados la mente humana no se corresponde
con la realidad de la naturaleza. De hecho, las observaciones de Newcomb y los
posteriores estudios de Bernford conducen a un resultado aparentemente sorprendente:
"Si disponemos de una cantidad suficientemente grande de datos numéricos
obtenidos de fenómenos naturales, el primer dígito no nulo de dichos
números es más probable que sea un 1 que un 2, más probable
que sea un 2 que un 3 y así sucesivamente. Es decir, a medida que aumenta
el primer dígito de la observación, disminuye la probabilidad. Además
este resultado es invariante frente a cambios de escala".
Para demostrar
esta hipótesis, Bernford partió de lo que hoy se conoce como
ley de Bernford: "El logaritmo de la mantisa de un número se distribuye
uniformemente entre 0 y 1".
Este resultado, obvio si tenemos en cuenta que la función logarítmica es estrictamente creciente y por tanto biyectiva entre [1,10] y [0,1], permite obtener fácilmente la función de densidad de probabilidad.
Antes de obtener la función de densidad vamos a considerar cada una de las observaciones obtenidas escritas en notación científica. Sea M la variable aleatoria continua que toma los valores de las observaciones obtenidas tomadas en dicha notación sin tener en cuenta la potencia de 10. Así la función de distribución de M será:
![]()
Por tratarse de una distribución uniforme, es a su vez igual a:
Entonces:
![]()
Por tanto,
la función de densidad de probabilidad será la derivada de la función
de distribución F(m):
Sin embargo, la distribución que queremos
estudiar es la del primer dígito no nulo de una observación. Pero
esta se calcula de manera sencilla recurriendo a la función de densidad
de M.
Sea D1(x) la variable aleatoria discreta referente al primer dígito no nulo de una observación. Su función de probabilidad será:
Es decir, la probabilidad de que el primer dígito no nulo sea 1 es igual
a 0.30103 diferente de la que nuestra intuición nos propondría:
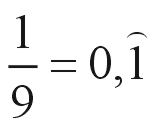
Para calcular la probabilidad de que el primer dígito no nulo sea 2 procedemos de forma análoga:
Así,
podemos calcular la probabilidad mediante ![]() la
relación:
la
relación:
n= 1,....9
Así, obtenemos la siguiente tabla que corresponde a las probabilidades del primer dígito:
Tabla 1: Probabilidades del primer dígito
Como
puede verse en la tabla 1 no son igual de probables todas las cifras como primer
dígito de un dato observado. Cuanto menor sea esta cifra ma-yor será
su probabilidad. Esto certifica las observaciones realizadas por Simon Newcomb:
se utilizan más las primeras hojas de las tablas de logaritmos, que eran
las que contenían los primeros dígitos.
Modelización estadística de la distribución del primer dígito
de la distancia de la Tierra a las estrellas
Para realizar este
estudio se ha extraído una muestra aleatoria de 500 estrellas y se ha obtenido
su distancia, en años luz, a la Tierra. Tanto la extracción de la
muestra como el cálculo de la distancia se ha realizado mediante el programa
informático STARRY NIGHT PRO.
Los resultados se muestran en el anexo 1. Cada estrella, numerada según el catálogo de Hipparcos, viene acompañada de su distancia a la Tierra, en años luz, y a continuación el primer dígito de dicha medida.
Las frecuencias relativas de los nueve dígitos se presentan en la siguiente tabla:
Tabla 2: Frecuencias relativas del primer dígito
Si comparamos las dos tablas podemos ver que efectivamente la similitud entre la distribución teórica y los datos obtenidos empíricamente es manifiesta. En el siguiente apartado se realizan dos contrastes de hipótesis que nos permiten evaluar la bondad del ajuste realizado. Este estudio nos permitirá concluir que la distribución estadística del primer dígito no nulo de la distancia de la Tierra a las estrellas sigue el modelo de la distribución de Bernford.
Estudio estadístico de los resultados obtenidos
Para estudiar si la distribución obtenida de forma empírica se ajusta a la distribución teórica propuesta por Bernford se realiza un análisis de la bondad del ajuste. Para ello se utilizarán dos métodos no paramétricos: el test de la y el test de KolmogorovSmirnov.
En
ambos casos se trata de realizar el contraste cuya hipótesis nula es:
H0: Los datos se extrajeron de una distribución de Bernford.
frente
a la hipótesis alternativa:
HA: Los datos no se extrajeron de una distribución
de Bernford.
El estadístico a considerar es:
que, cuando la hipótesis
nula es verdadera, se distribuye como una con 9-1 grados de libertad.
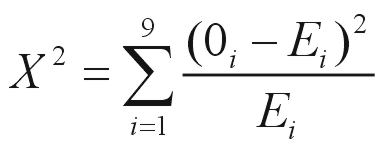
En la expresión anterior Oi se refiere a la frecuencia absoluta observada cuando el primer dígito es i y Ei, a la frecuencia absoluta esperada para dicho dígito según la distribución de Bernford.
Al
determinar los grados de libertad, se resta una unidad al número de grupos
puesto que se impone una restricción:
Así, la tabla 3 permite
obtener el valor de X2:
Tabla 3: Cálculo del estadístico X2
Tabla
3. Calculo estadistico de![]()
Es decir, ![]() =
5.4711107. Para un nivel de significación a=0.05, el valor de con 8 grados
de libertad es 21.955 de manera que no puede rechazarse la hipótesis nula
al nivel de significación considerado o a cualquier otro nivel de significación
razonable (p>0.1). Esto significa que no hay ninguna evidencia para no poder
afirmar que los datos obtenidos siguen la distribución propuesta por Bernford.
=
5.4711107. Para un nivel de significación a=0.05, el valor de con 8 grados
de libertad es 21.955 de manera que no puede rechazarse la hipótesis nula
al nivel de significación considerado o a cualquier otro nivel de significación
razonable (p>0.1). Esto significa que no hay ninguna evidencia para no poder
afirmar que los datos obtenidos siguen la distribución propuesta por Bernford.
A continuación se realiza un estudio similar mediante el contraste de Kolmogorov-Smirnov.
Este es un test que, al igual que el anterior, se utiliza para comprobar si una muestra de datos procede de una determinada distribución teórica.
Así como el test de la utilizaba las frecuencias absolutas para la comparación de las distribuciones, la prueba de bondad de ajuste de Kolmogo-rov-Smirnov se vale de las frecuencias relativas acumuladas. Es decir, se compara una función de distribución acumulada y teórica FT(x) y la función de distribución acumulada de una muestra F(x).
La diferencia entre la función de distribución acumulada y teórica, FT(x), y la función de distribución acumulada de la muestra, F(x), se mide me-diante el estadístico D, que es la diferencia máxima entre ambas distribuciones.
Las suposiciones que fundamentan la prueba son la aleatoriedad de la muestra y la continuidad de la función de distribución teórica.
La segunda condición no se cumple en nuestro caso. Sin embargo, Noether ha demostrado que cuando los valores de D se basan en una distribu-ción teórica discreta, la prueba es conservadora. A tenor de los resultados obtenidos, recogidos en la tabla 4, dicho conservadurismo no influye en la decisión final pues el margen obtenido para no rechazar la hipótesis de igualdad de las dos distribuciones es muy amplio.
Tabla 4: Cálculo del estadístico D
Es decir, D=0.02097. Este valor si se compara con los valores que obtenemos en una tabla del test de Kolmogorov-Smirnov no es significativo a cualquier nivel razonable.
A modo de conclusión
Se ha expuesto un hecho aparentemente increíble para nuestra lógica concepción del Universo. La deseada uniformidad no existe. Sin embargo, la curiosidad humana ha sido capaz de descifrar esta supuesta controversia.
Todo lo anteriormente expuesto no es un ejemplo aislado y casual sino que como Bernford expuso se trata de un fenómeno natural.
Ya lo dijo Galileo hace algunos siglos,
"la matemática es el lenguaje con el que Dios ha escrito el Universo".